The reactor plasma system manages the ‘triple product’ necessary to maintain a self-sustaining fusion reaction: plasma density, temperature and energy confinement time. There are therefore three critical components within the plasma system.

The point at which the reaction produces more energy than it loses is referred to as ignition. Until ignition, plasma temperature is raised using external energy sources until the point where the reaction’s energy is sufficient to sustain itself.

Reaction 'Triple-Product'

For a fusion reaction to overcome radiation losses and become self-sustaining, a 'triple product' of plasma temperature, density and confinement time are required. This is referred to as the Lawson Criterion.

There are therefore three critical response profiles within the plasma simulation.

The point at which the reaction produces more energy than it loses is described as ignition.

Plasma Creation

[STUB] There is an initial process to create 'cold' plasma that the reaction ignition system can warm up. Link to separate system article.

Plasma Density

Plasma density is a function of the amount of fuel plasma relative to the volume of the space containing it (the effective Reaction Volume (eRV)). Adequate plasma density is critical to maintaining a self-sustaining reaction. The main containment field is used to compress plasma so as to significantly increase density.

Increased plasma density forces plasma particles into greater proximity and thereby increases the likelihood of particle collision which increases plasma temperature.

Similarly, increased plasma density also increases the likelihood of collision between plasma and particles created by the fusion reaction process. This increases confinement time (See below).

Plasma density can be expressed in numerous forms but the most useful for fusion reaction purposes is to measure electron density. This is expressed as particles per cm³ (e-cm³).

Function

The plasma density function is a ratio of the amount of fuel isotope to the effective reaction volume. The standard volume that the isotopes would normally take up is calculated, then the actual volume available is calculated against this to determine the density:

Where F is the amount of fuel isotope in the segment (see plasma fuel level below), W is the weight of hydrogen and r is the minor radius (see segment effective reaction volume below).

Future Expansion

Plasma density does not fully reflect the pressure the plasma will place on the containment field. As plasma temperature increases, the standard volume taken up by the fuel isotopes would also increase as the increased energy of particles pushes them further from each other.

This has not been taken into account in the current version of the simulation, in order to simplify the algorithm for testing and initial deployment. Future updates to the simulation may look to add this to the algorithm.

Segment Effective Reaction Volume

The Effective Reaction Volume (ERV) describes the volume contained within the main containment field (see the toroidal simulation overview for more details on the ERV).

As each toroidal generator might have a different power output (and therefore a different ERV), to allow the plasma system to operate on a segment basis the ERV of each toroidal generator is split at the generator (22.5 degrees from the segment meridian) and added to output from the facing toroidal generator.

This calculates the Segment Effective Reaction Volume (segERV).

Plasma Fuel Level

Reaction plasma is made up of superheated and ionised hydrogen isotopes – deuterium and tritium. The Plasma Fuel level measures the amount of hydrogen isotopes currently available.

Measured in gm/m³

Plasma Burn

The reaction process converts these isotopes into helium which eventually escapes the reaction as helium ash. This hydrogen entropy is described as ‘plasma burn’. Additional isotopes need to be introduced to the plasma to compensate for plasma burn.

Function

Plasma burn is described by the function:

where x is the plasma temperature, s is the scale, m is a modifier and r is the range (which modifies the burn rate by a factor of 10).

Plasma Balance

An optimal balance between constituent isotopes ensures reaction efficiency. Deuterium-tritium fusion is the most efficient, occurring at lower temperatures. If Tritium levels drop, this decreases the likelihood of this kind of reaction and increases the likelihood of a deuterium-deuterium reaction or even a deuterium-helium reaction.

Plasma Fuel Injection System

Separate system, brief overview and link here.

Plasma Temperature

Plasma temperature is the key user-observable output from the reaction plasma system and measures the amount of energy currently in the reaction.

The containment time (see below) determines how much energy is added to or lost from the reaction. This will cause plasma temperature to rise or fall accordingly.

Plasma temperature is measured in megakelvins (mK).

External Energy Input

In order to get plasma to ignition temperature, external energy must be introduced by the Reaction Inginition System (RIS). 

Function

Energy output from the RIS is converted to plasma temperature at a ratio of approximately 1eV:11604K.

where E is the energy added to the plasma temperature (in degK), N transferred from the RIS and K is the conversion modifier from eV to degK.

Plasma Temperature Function

Plasma temperature is described by the function:

Where P is the current plasma temperature, E is the energy transferred from the RIS and C is the energy retained (as desribed by the Energy Confinement Time - see below).

Confinement Time

Energy confinement time is a measure of how well a reaction retains energy. The products of an individual reaction (two hydrogenic nuclei fusing) are alpha particles (helium nuclei) and neutrons, with each possessing kinetic energy. Neutrons produced by fusion are high-speed particles, possessing four times the kinetic energy of alpha particles.

Ideally, this kinetic energy is transferred to the plasma’s hydrogenic particles to induce subsequent reactions. The ability to maintain this ‘chain reaction’ is critical to a self-sustaining reaction. As both alpha particles and neutrons have no electrical charge, they cannot be contained by the reactor’s magnetic fields and so will escape the reaction. The reaction’s ability to extract as much kinetic energy before particles escape determines confinement time (thus the term).

Conduction

The primary form of energy loss from a fusion reaction is therefore conduction, which occurs when a particle escaping the reaction impacts a surface (the reactor chamber wall), thereby transferring their kinetic energy to the surface. The modules making up the Reaction Isolation Shield (RIS) use this to create thermal energy which is transferred to the primary coolant loop to drive the generation process. Alternatively, some RIS modules use neutronic impacts to breed tritium.

Radiation

Energy is also lost through radiation, in the form of light in the visible, UV, IR or gamma/X-ray spectrum.

NOTE: Vacuum and purity (ie no helium ash) also factors in efficiency. Handled as discrete variables for now?

Response Profile

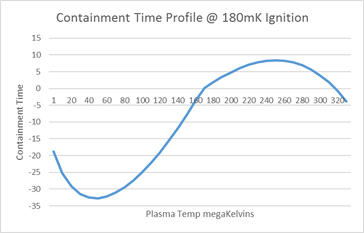Energy confinement time describes how efficiently energy is retained within the reaction.

Ideally as much energy should be transferred from a fusion event to surrounding plasma before being lost from the reaction in the form of EM radiation or escaping neutrons.

Confinement time measures net energy retained within the reaction over a given period of time (to be defined). Where this is negative, energy is being lost from the reaction.

Confinement time is the reaction energy level modified.

Reaction energy E for current plasma temperature x is calculated as:

Where i is the ignition temperature (see below), r is reactivity (see below) and d is plasma density delta (from standard).

Energy level E is then modified to produce confinement time C by subtracting from it the current plasma temperature (x), to give the confinement time:

Modifiers

There is a distinct inflection point at ignition, reflecting the fact that additional energy is being supplied by the reaction itself and not the Reaction Ignition System (RIS).

Where plasma temperature x is above the ignition temperature i, a post-ignition modifier is applied:

where d is plasma density (see below), p is a constant and r is reactivity (see below)

Operating Factors

Cross-Section/Reactivity

Reaction cross-section measures the probability of a fusion reaction as a function of the relative velocity of the two reactant nuclei. Where there is a distribution of velocities (ie the thermal distribution within the reactor) then an overage over distributions is a more useful measure. This measure is reactivity, measuring fusions per volume per time.

Reactivity is measured in m³/sec.

Reactivity is calculated as the logarithm of plasma temperature with a base of the ignition temperature i:

Ignition

Reaction ignition describes the point where the reaction produces more energy than it loses, thereby becoming self-sustaining (without external energy input). The ignition temperature will vary with plasma density.

The ignition point is calculated as:

Where b is a constant describing the base ignition temperature for the plasma’s isotope mix, m is a modifier which determines the responsiveness of the function to changes in density, and d is plasma density delta (from standard, which is one ie 1 - d).

Output

The ECT value output from the Confinement Time component is added to the current Plasma Temperature after the required period has elapsed. Below ignition, the ECT value will be negative, resulting in a reduction in plasma temperature.